来源:TSNLAB 微信公众号
TSN技术来源于工业自动化、音视频桥接网络等,上述场景存在业务对网络时延上界、可靠性有明确要求。TSN定义了一套工具集:包括时间同步、整形和调度、资源预留机制等,来提供零丢包、有界时延能力。然而,对于一个具体业务,时延上界能否在多跳传输网络上满足?对时间门控类调度,编排算法保证了时延上界保证;对基于带宽分配的异步调度,网络演算是时延上界估计和网络资源分配的理论依据。
Motivation:网络SLA需求
5G、云、物联网等新技术的发展与应用,在为人类的生产与生活带来新的通信体验的同时,也对网络服务提出了新的需求。具体地,多种新的业务场景需要差异化的SLA(服务等级协议,ServiceLevel Agreement)保障,时延保障是其中重要的一项。
5G超高可靠低时延通信(ultra-Reliable Low-LatencyCommunications, uRLLC),顾名思义,对网络提出了低时延的要求。其主要面向工业与智能制造、电力、车联网、金融等垂直行业的特别需求,对时延的要求一般也在毫秒级。IEEE 802.1 TSN DG profile for vehicle 定义了典型业务的时延上界需求,如下图所示,其中TC8命令、控制类业务时延上界需求在1ms,TC6视频类业务的时延上界在16ms。
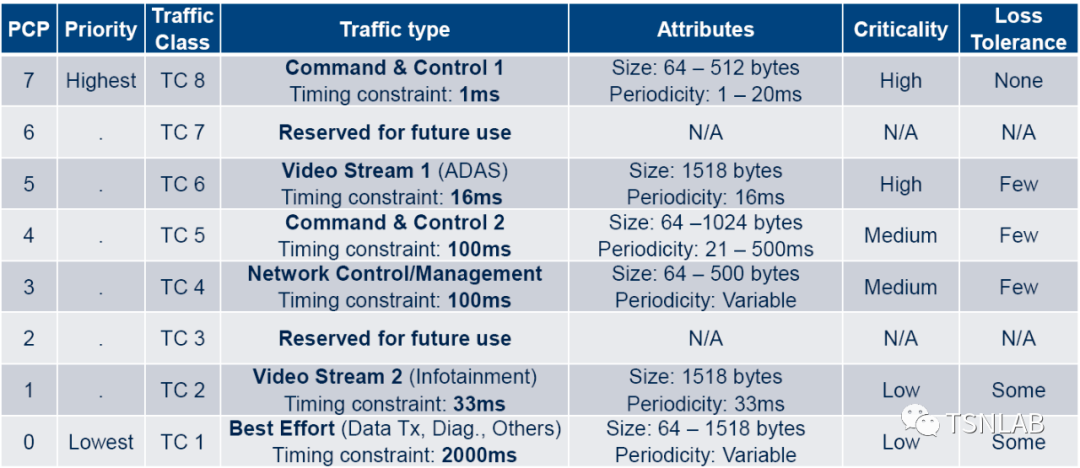
Latency requirement for each traffic class in 802.1DG [1]
众所周知,网络中多流汇聚时的微突发是排队时延的主要来源,如何保证大量流量在最差突发汇聚的排队冲突下,仍然能够满足业务时延需求?
TSN网络设计的要解决这个关键问题:根据流量特征、网络拓扑、时延需求,来选择合适的TSN调度机制和配置。一般来说,对于极低时延、周期类流量,例如TC8,可以采用时间门控调度,后续文章会介绍TSN TAS的编排算法;对于低时延高可靠需求、随机突发的流量,如音视频流量TC6,可采用TSN CBS、ATS等异步调度,此时的网络时延上界估计将用到网络演算。
Theory:网络演算
网络演算(Network Calculus)又译为网络微积分(下文均称网络演算)。网络演算是用于分析如通信网络、数字电路、并行程序等人造系统的一种数学方法,主要分析目标是时延等“服务保障(performance guarantees)”。网络演算最初由R. L. Cruz在1990年提出[2][3],此后迅速发展[4][5]。
网络演算主要由以下关键部件组成:
•流量建模:使用到达曲线(Arrival Curve)描述流量到达网络设备时的行为特征,典型用法是描述任意时间到达数据量的上界。
•网络服务建模:使用服务曲线(Service Curve)描述网络设备的服务能力,重点是对调度器行为的描述,典型用法是描述任意时间内网络服务能力的下界(minimumservice curve)。
•计算方法:考虑网络拓扑、流量间的相互干扰等,计算任意一个流量在网络中传输的端到端时延上界。
通过建立到达曲线和服务曲线,网络演算可以把复杂的网络系统转变为易于分析、级联的、在(min,plus)代数域上的线性系统,进而可进行机器计算求解。
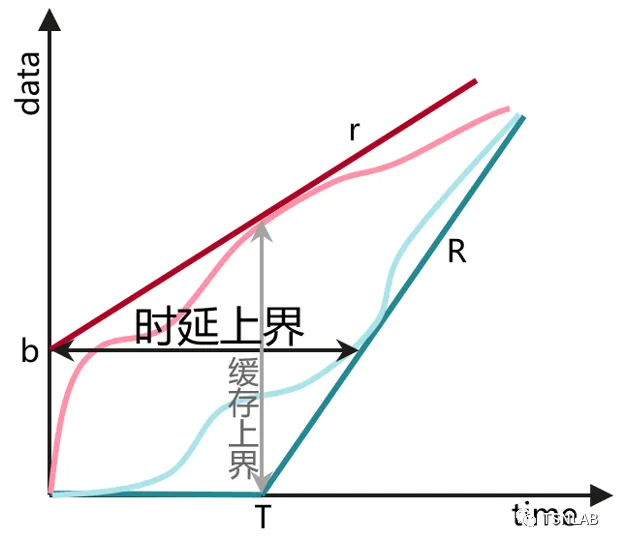
时延上界与缓存上界示例
目前网络演算的主要技术分支有:
•确定性网络演算(DeterministicNetwork Calculus, DNC),基于到达曲线和服务曲线,计算100%保障的时延上界,如端到端最坏时延不会超过10ms。[5][6]
•随机网络演算(Stochastic Network Calculus,SNC),考虑流量到达和/或网络服务的随机特性,计算一定可靠性性概率下(例如99.99%)的时延上界。[7][8]
学术界对于网络演算研究的应用场景从最初ATM网络,发展到IP网络,目前网络演算最成功的商业应用案例是在机载网络(AFDX,Avionics Full DupleXswitched Ethernet)[9][10],正在逐渐扩展到工业网络、车载网络,以及无线网络等时延上界敏感的应用场景。
Application: 网络演算用于TSN调度
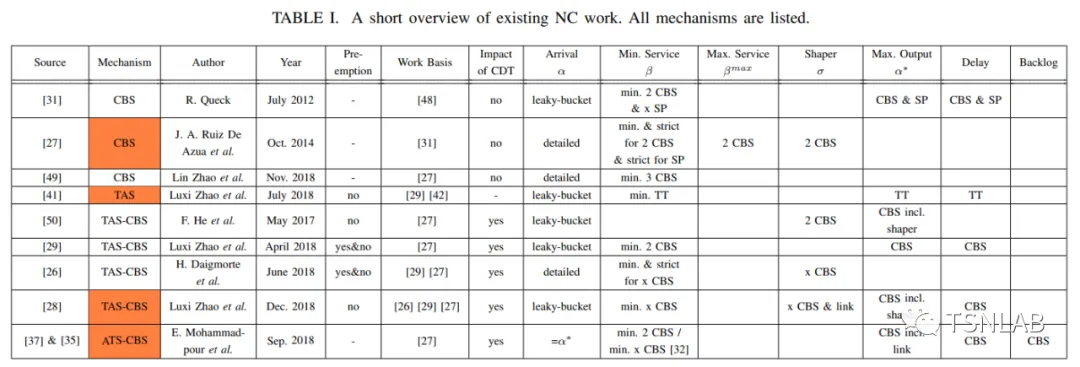
TSN调度及其组合列表 [11]
根据TSN标准定义的数据面调度机制,调度及其组合的服务器曲线在文献[11]中被推导。其中流量模型可参考TSPEC给出。而TSN的端到端时延上界可计算。下面介绍两种典型异步调度:CBS、ATS的服务曲线。
1 CBS
在AVB网络中,主要设置两类优先级流量进行CBS(Credit Based Shaper)整形,即Class A和Class B流量(A的优先级高于B);Class A和Class B流量在传输排队时依赖两个带宽保障参数idleSlopeA/B和sendSlopeA/B,其中,idleSlopeA/B是ClassA/B流量在节点处等待传输时信用量的增加速率,sendSlopeA/B是Class A/B流量正在传输时信用量的减小速率,C为链路的总带宽传输速率。
流量在Talker处以周期T时间产生并发送进入网络的流量可建模为(r,b)漏桶模型,以及考虑到网络链路总带宽C的输出约束能力;流量到达使用到达曲线描述,周期性流量到达曲线定义为,
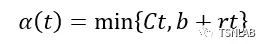
其中,b为流量的最大突发量,一般可认为是流量的最大帧长LA/LB;r为流量的最大可持续稳定速率,由此得出到达曲线。
下面给出服务曲线描述。具体而言,对A类流量,
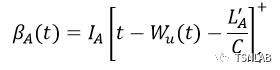
对B类流量,
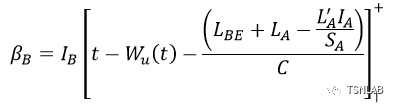
其中,IA、IB分别为idleSlopeA、idleSlopeB,SA为sendSlopeA;LA、LB、LBE分别代表A、B、BE类最大帧长,L'A代表优先级低于A类流量的最大帧长,也即L'A=max{LB, LBE};Wu(t)代表为CDT类分配的时间窗口上界。
2 ATS
ATS(AsynchronousTraffic Shaper)是一个异步数据流整形器,它旨在通过每跳重塑TSN数据流,ATS并不要求桥和终端节点同步,对于高实时要求和非实时业务混合业务模式下,ATS也能保持带宽的最大利用率。ATS采用基于令牌桶的核心算法将合格时间分配给属于特定流的帧,然后由ATS传输选择算法用于流量调节。
ATS采用的核心算法ATS算法是基于令牌桶算法进行流量整形,该整形器为一个贪婪整形器,对于每一类流量,令牌桶中令牌量和增长速率是相对独立的,所以对于各类型流量来说,ATS对其提供的整型曲线(服务曲线)为:
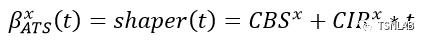
ATS所提供的整形曲线受CBSx和CIRx两个参数影响,参数的配置决定了ATS的服务能力。但如果ATS所提供的整形曲线小于流量的到达曲线,也就是整形器的服务能力要小于流量的到达,ATS也会按整形曲线对流量整形,但需要付出延迟的代价,此时流量经过ATS所产生的延迟为:
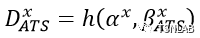
流量离开的突发由整形器限制,即:a*(t) = min{a(t), shaper(t)},作为下一跳的到达曲线。据此可以计算端到端时延上界。
案例分析
[12]研究了一种优先级配合CBS的方案,并使用确定性网络演算进行了时延分析。具体地,其拓扑包括两个生产单元、15个节点,共116-232条流根据其业务的时延需求分为4个等级。4个等级之间按绝对优先级调度,而等级2和3额外使用了CBS机制。时延分析结果如下图 所示,表明了在该调度方案的设计下,各类流量的传输时延需求均得到了满足。这也说明,CBS这类不依赖于时间同步的调度方式可以用于工业自动化网络,提供时延保证。
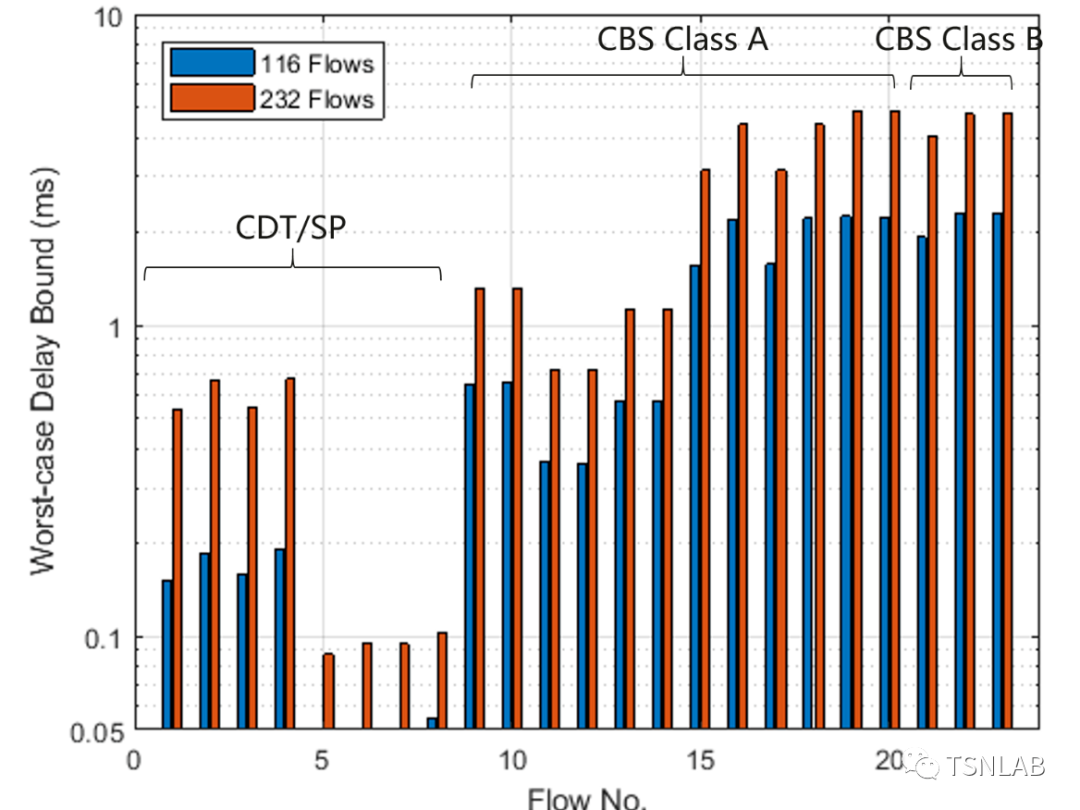
一个工业自动化网络案例下的网络演算时延分析结果 [12]
作者按:长期以来,异步调度之前面向的业务更多是best-effort,而非精准规划。随着研究的推进和应用场景的推广,越来越多的同事和客户能够接受在保证可靠时延上界,“时延上界理论值比实测测量结果(平均值)大挺多”,“带宽规划理论值比平均带宽大不少”。谁让突发、带宽和时延是一组此消彼长的三角关系。
感兴趣的同学可以关注华为数据通信基础理论系列的新书《网络演算-互联网确定性排队系统理论》,是本领域经典教材[5]的中文译本首次出版。读者能够了解到突发、服务如何影响到确定性时延,从严格数学理论到经典案例应用。
作者简介
张嘉怡博士,华为公司数据通信产品线 研究工程师, 负责网络性能评估、网络演算理论、算法及确定性网络技术研究。2018年毕业于清华大学电子工程系获博士学位。
参考文献
[1].IEEE 802.1 TSN Profile forvehicle network, dg-gopal-TrafficClass-text-1021-v02
[2].R. L. Cruz, "A calculusfor network delay. I. Network elements in isolation," in IEEE Transactionson Information Theory, vol. 37, no. 1, pp. 114-131, Jan. 1991, doi:10.1109/18.61109.
[3].R. L. Cruz, "A calculusfor network delay. II. Network analysis," in IEEE Transactions onInformation Theory, vol. 37, no. 1, pp. 132-141, Jan. 1991, doi: 10.1109/18.61110.
[4].C.-S. Chang: “PerformanceGuarantees in Communications Networks,” Springer, 2000.
[5].J-Y. Le Boudec and P. Thiran, “Networkcalculus: a theory of deterministic queuing systems for the internet,” Vol.2050, Springer Science I&Business Media, 2001.
[6].A. Bouillard, M. Boyer, and E.Le Corronc, “Deterministic Network Calculus: FromTheory to Practical Implementation,” Wiley-ISTE, 2018
[7].Y. Jiang and Y. Liu, “StochasticNetwork Calculus,” Springer, 2008.
[8].M. Fidler and A. Rizk, "AGuide to the Stochastic Network Calculus," in IEEE Communications Surveys& Tutorials, vol. 17, no. 1, pp. 92-105, Firstquarter 2015, doi: 10.1109/COMST.2014.2337060.
[9].F. Frances, C. Fraboul, and J.Grieu, "Using Network Calculus to optimize AFDX network,” in Proceeding ofthe 3thd European congress on Embedded Real Time Software (ERTS06), January2006, Toulouse.
[10].M. Boyer and C. Fraboul, "Tightening end to end delay upperbound for AFDX network calculus with rate latency FIFO servers using networkcalculus," 2008 IEEE International Workshop on Factory CommunicationSystems, Dresden, 2008, pp. 11-20, doi: 10.1109/WFCS.2008.4638728.
[11].L. Maile, K. Hielscher and R. German, “Network Calculus Results forTSN: An Introduction,” 2020 Information Communication Technologies Conference(ICTC), 2020, pp. 131-140, doi: 10.1109/ICTC49638.2020.9123308.
[12].J. Zhang, L. Chen, T. Wang and X. Wang, "Analysis of TSN forIndustrial Automation based on Network Calculus," 2019 24th IEEEInternational Conference on Emerging Technologies and Factory Automation(ETFA), 2019, pp. 240-247, doi: 10.1109/ETFA.2019.8869053.