摘 要：为了克服常规PID稳定范围较小、适应性及鲁棒性较差及微分信号难于提取等缺陷，应用非线性控制理论，基于非线性跟踪微分器及PID校正的思想，设计了一种用于静止无功补偿器(SVC)的新型非线性PID控制器。这种控制器具有不依赖于被控系统知识的特点，对系统工作点和网络结构的变化具有良好的鲁棒性且结构简单，易于实现。数值仿真结果表明，这种非线性PID控制器的控制品质好，不但能有效地改善电力系统功角稳定性和SVC安装点的电压动态特性，而且具有较强的适应性和鲁棒性。

　　1 引言

　　非线性PID控制器的调节原理为：利用参考输入和系统输出的偏差及其微分、积分的非线性组合来产生控制信号，利用非线性特性来改善被控系统的稳态偏差及暂态过程。非线性PID控制器的框图如图1，图中，虚线框部分为非线性PID控制器;v0(t)为系统的参考输入;u(t)、y(t)分别为系统的控制输入、输出; 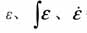分别为偏差、偏差的积分和偏差的微分。

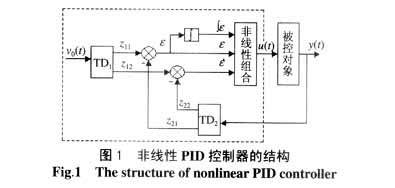
　　跟踪-微分器[4, 5]TD1用于给出v0(t)理想的过渡过程z11(t)，并给出理想的过渡过程微分信号z12(t)，其中的参数根据过渡过程的快慢要求而定;跟踪-微分器TD2主要尽快复原y(t)并给出其近似微分，因此，其中的参数要取足够大。利用2个跟踪-微分器，即可解决经典的线性PID控制器中微分信号不易提取的问题。

　　基本要素的非线性组合是为了解决线性组合带来的超调和快速之间的矛盾。确定非线性组合的一个基本标准是：和线性组合相比，偏差小时，采用较大控制;偏差大时，采用较小控制。

　　非线性PID控制器的参数只取决于对象的结构。某一特定对象调好了，按照一定的目标或原则，就能找出适应性、鲁棒性很好的一组参数[5, 6]。

　　3 SVC非线性PID控制器的设计

　　3.1 数学模型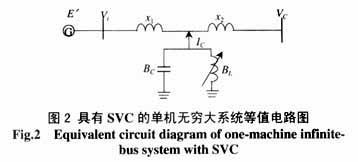

　　具有SVC的单机无穷大系统等值电路图如图2所示。假设发电机采用经典二阶模型，恒定。其数学模型为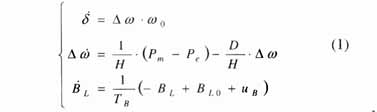

　　式中 d为发电机转子摇摆角;Dw为发电机转子角速度增量;w0为系统同步角速度;D为发电机阻尼系数;H为发电机组转子的惯性时间常数;Pm为发电机机械功率;uB为SVC控制的输入;TB为SVC及调节系统的惯性时间常数;BL为SVC中可调电感等效电纳值;BL0为SVC中可调电感初始电纳值;Pe为发电机输出的电磁功率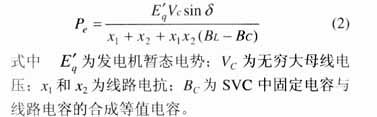

　　3.2 用于SVC的非线性PID控制器的设计

　　将式(1)改写成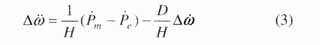

　　式(7)所示为一平滑仿射非线性系统，通过一定的坐标变换，采用反馈线性化方法使其转化为线性系统，以利于控制器的设计。采用微分几何理论或直接线性化方法可选取最终坐标变换为

　　将式(8)、(9)代入式(10)，得到SVC的非线性反馈补偿规律为

　　式中 z1、z2、z3为反馈线性化模型的状态变量，v为模型的虚拟控制变量。

　　虚拟控制量v应针对反馈线性化后的标准型设计，理论上已证明，反馈线性化后的系统与原系统具有相同的能控性。可以看出，无论发电机的工作点如何变化，式(11)在形式上是不变的，从而保证了非线性PID型SVC控制器对系统工作点的变化具有较好的鲁棒性。另一方面，为了使控制器对于系统网络结构的变化具有较强的鲁棒性，在式(13)中选取z2即发电机角速度误差变量Δω为反馈变量，构成动态反馈补偿，则变换后的发电机角速度误差变量表达式为

　　式中 δ为决定fal(Δω,α,δ)函数线性区间大小的参数;α为决定该函数的非线性形状的参数(非线性度)。

　　利用MATLAB仿真工具试算，对比多组不同线性区和非线性度的计算结果，综合考虑系统指标改善程度和预防系统发生高频颤振现象的需要，确定a =0.4，d =10-4。

　　为了使发电机达到快速稳定，非线性PID控制的目标必须使发电机功角和角速度尽量同时趋近于稳态值，即兼顾Z1(Δδ/ω0)和z2(Δω)尽快趋近于零，为此，利用MATLAB仿真工具的多次试算进行参数的优化选择，在上述条件(a, d)下，获得z1和z2性能较好且系统增益较小的一组PID参数值为：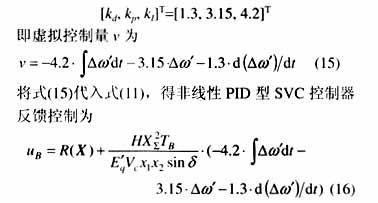

　　4 数值仿真分析

　　仿真系统如图3所示，发电机及网络参数为: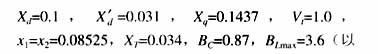

　　上各量的单位均为标幺值)，H=42 s，Td0=10.2s。仿真条件为：系统于t =0.1 s在F点发生三相短路故障, t =0.18 s故障消除, Pe=7.0。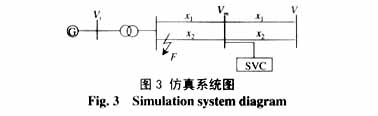

　　图4给出了系统在常规SVC控制器和非线性PID型SVC控制器作用下的响应曲线，其中, 实线和虚线分别对应在非线性PID型SVC控制器和常规SVC控制器作用下的响应曲线。